Introduction to Kolmogorov-Arnold Networks (KANs)

You might be familiar with the Multi-Layer Perceptron (MLP) neural network architecture, a cornerstone of deep learning. But now, there’s a new contender making waves in the field — introducing Kolmogorov-Arnold Networks (KANs)! Based on the Kolmogorov-Arnold Representation Theorem, KANs offer a revolutionary approach to neural network design. Recently introduced on April 30th, these models are set to transform the way we tackle complex data patterns and conduct deep learning. KANs utilize smooth polynomial basis functions called splines, which significantly enhance performance when applied effectively. Before we delve into the KAN model, let’s take a moment to revisit MLPs. By refreshing our understanding of MLPs, we can better appreciate the significance of KANs!

What are Multi-Layer Perceptrons (MLPs)?

Multi-Layer Perceptrons (MLPs) are a foundational type of artificial neural network commonly used in deep learning. An MLP consists of multiple layers of nodes, or neurons, arranged in a feedforward structure. Each neuron in a layer is connected to every neuron in the next layer, with these connections weighted to represent the strength of the influence of one neuron on another.

Here’s a quick breakdown of MLP components:

• Input Layer: Receives raw input data.
• Hidden Layers: Intermediate layers where neurons apply activation functions to transform inputs and pass them to the next layer.
• Output Layer: Produces the final output of the network.

MLPs use nonlinear activation functions, like the sigmoid, tanh, or ReLU, allowing them to model complex relationships in data. They are trained using backpropagation, an algorithm that adjusts weights to minimize the difference between the predicted and actual outputs. This makes MLPs versatile tools for various tasks, including classification, regression, and pattern recognition. Now, let’s review the inspiration behind these KAN models:

The Kolmogorov-Arnold Representation Theorem

The Kolmogorov-Arnold Representation Theorem is a mathematical principle that simplifies multi-variable functions into basic single-variable functions connected through addition operations. Picture calculating the volume of a complex 3D object composed of multiple shapes. Instead of determining the formula for each shape, you break the problem into simpler parts and sum them up. This approach reduces complexity, making it easier to solve high-dimensional problems using smaller, more manageable components.

Understanding Kolmogorov-Arnold Networks (KANs)

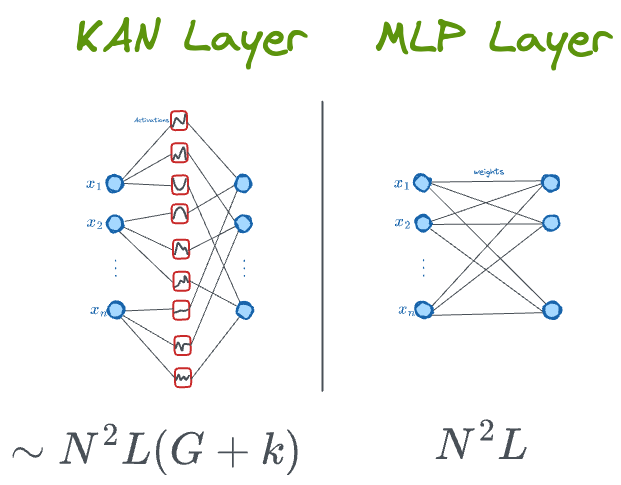
KANs are inspired by the Kolmogorov-Arnold representation theorem. Unlike traditional Multi-Layer Perceptrons (MLPs) with fixed activation functions at each node, KANs use learnable activation functions on each connection between nodes. Rather than relying on single weight parameters, KANs employ splines — flexible functions that capture complex relationships between inputs and outputs. This leads to higher accuracy and easier result interpretation. Furthermore, KANs offer more efficient scaling compared to MLPs, making them suitable for a variety of problems.

KANs are composed of three primary elements: input nodes, hidden splines, and output nodes. Unlike other neural networks that use fixed activation functions, KANs use splines — flexible 1D functions — along connections between nodes. These splines enable KANs to learn intricate relationships between inputs and outputs, particularly when dealing with compositionality.

• Input Nodes: These nodes receive raw data and pass it to the hidden splines.
• Hidden Splines: Represented as curved lines through sets of points, these splines capture higher-order derivatives without adding more layers or parameters.
• Output Nodes: These nodes calculate a weighted sum of all activations from the hidden splines and deliver the final result.

KANs vs. MLPs: Which to Choose?

Another aspect to understanding KANs is understanding the differences between KANs and MLPs which can help you decide which model is best for your needs.

Data Size and Computational Resources

• Small Datasets: KANs are advantageous for smaller datasets due to their lower memory footprint and better numerical stability.
• Large Datasets: For larger datasets, MLPs’ efficient batch processing can be more effective, especially with powerful hardware.

Interpretability vs. Accuracy

• Interpretability: KANs offer explicit function representation, making them more interpretable. This is beneficial when understanding the model’s behavior is crucial.
• Accuracy: MLPs might be preferable if accuracy is the primary goal, as they can sometimes train faster and handle larger datasets more efficiently.

Efficiency and Flexibility

KANs allow for more efficient learning and can capture complex patterns with fewer parameters. They also enable grouping activation functions into multiple heads, which reduces training time while maintaining flexibility.

Hybrid Approaches

Combining the strengths of KANs and MLPs can lead to higher performance and better interpretability. Leveraging the interpretability of KANs with the efficient processing of MLPs offers a balanced solution.

In conclusion, the emergence of Kolmogorov-Arnold Networks marks a pivotal moment in the landscape of neural network architectures. With their ability to capture intricate relationships and handle compositionality, KANs offer a promising pathway to enhanced accuracy and interpretability in machine learning. I hope you enjoyed my interpretation and summary of KANs!

Resources:

PDF link; Research Link;